Answer:
Option C is correct.
as x > 0 increases, f(x) increases,
as x < 0 decreases, f(x) increase.
Explanation:
Given the function:
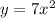
Degree of the polynomial states that the sum of the exponents of each variable in the expression.
The degree of
 is 2 i.e Even
is 2 i.e Even
The leading coefficient of the polynomial
 is, 7 i.e, Positive.
is, 7 i.e, Positive.
End behavior of the polynomial is the behavior of the graph of f(x) as x approaches positive infinity or negative infinity.
Also, the degree and the leading coefficient of a polynomial function determine the end behavior of the graph.
Since, the degree of the given function is even and the leading coefficient is positive.
End behavior of the function
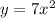 is:
is:
as
 , then
, then

and
as
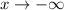 , then
, then

Therefore, as x > 0 increases, f(x) increases.
As x < 0 decreases, f(x) increases.