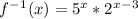Answer:
The answers are:
Graph: in the attached image
Inverse function:
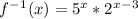
Explanation:
In order to get the graph with both functions, we have to determine the inverse function of
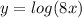
The steps are:
- we have to free the "x" variable.
- Then we have to invert the "y" and "x" variables.
- Finally, the "y" variable is called
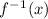
So, first, we applicate the next property:
If
 , so
, so
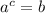
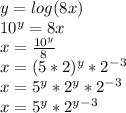
Then, we invert the variables:
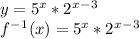
I have attached an image that shows the graph of both functions.
In red:
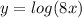
In blue: