Using complete sentences, explain the key features of the graph of the tangent function.

Question

asked Nov 20, 2017 9.1k views

1 Answer

Benedictanjw · Answer 1 · 2017-11-26T02:35:26+0000

Answer:

We are given the tangent function
$f(x)=\tan x$ .

Firstly we know that,
$\tan x=(\sin x)/(\cos x)$ , where
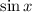$\sin x$ is the sine function and
$\cos x$ is the cosine function.

Now, tangent function will be zero when its numerator is zero.

i.e.
$\tan x=0$ when
$\sin x=0$ .

i.e.
$\tan x=0$ when
$x=n \pi$ , where n is the set of integers.

So, tangent function crosses x-axis at
$n \pi$ , n is the set of integers.

Further, tangent function will be undefined when its denominator is zero.

i.e.
$\tan x=0$ when
$\cos x=0$ .

i.e.
$\tan x=0$ when
$x=(2n-1) (\pi)/(2)$ , where n is the set of integers.

Moreover, a zero in the denominator gives vertical asymptotes.

So, tangent function will have vertical asymptotes at
$(2n-1) (\pi)/(2)$ , n is the set of integers.

Therefore, these key features gives us the graph of a tangent function as shown below.