Question

The point (8, –15) is on the terminal side of an angle θ. What is sin θ ?

Answer 1

`\sin \theta = -(15)/(17)`

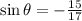
Explanation:

Given the point (8, -15) is on the terminal side of an angle
`\theta`.

To find the value of
`\sin \theta`.

As the point (8, -15) lies in the fourth quadrant where
`\sin \theta < 0`

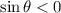
In a right angle triangle;

here, adjacent side = x = 8 units and Opposite side = y = -15 units

Using Pythagoras theorem;

`(Hypotenuse side)^2 = (Adjacent side)^2+(Opposite side)^2`

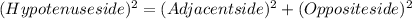
Substitute the given values we have;

`(Hypotenuse side)^2 = (8)^2+(-15)^2`

`(Hypotenuse side)^2 = 64+ 225 = 289`

`Hypotenuse side = √(289) =17 units`

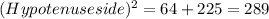
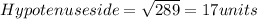
Sine ratio is defined as in the right angle triangle, the ratio of opposite side to Hypotenuse side.

`\sin \theta = (Opposite side)/(Hypotenuse side)`

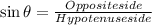
then;

`\sin \theta = -(15)/(17)`

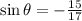
therefore, the value of
`\sin \theta` is
`-(15)/(17)`.

Answer 2

For the answer to the question What is sin θ ? (8, -15) is in quadrant IV.

Draw the right triangle.
hypotenuse = √(8² + 15²) = 17
sinθ = -15/17

Just draw the graph for reference.

I hope my answer helped you. Feel free to ask more questions. Have a nice day!