Question

If you tripled the slant height and radius of a cone, what would be the formula to find the modified surface area?

Answer 1

Hence, the formula to find the modified surface area is:

`9(\pi r^2+\pi rl)`

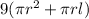
i.e. it is 9 times the surface area of the original cone.

Explanation:

We know that the surface area of a cone is given by the formula:

`Surface\ Area(S)=\pi r^2+\pi rl`

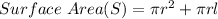
where r is the radius of the cone and l is the slant height of the cone.

Now we have that:

The slant height of the cone is tripled and the radius of a cone is also tripled.

i.e. r=3r

and l=3l

Hence, the modified surface area is given by:

`Surface\ Area(S')=\pi (3r)^2+\pi (3r)\cdot (3l)\\\\\\S'=9\pi r^2+9\pi rl\\\\\\S'=9 (\pi r^2+\pi rl)\\\\\\S'=9 S`

Answer 2

For the answer to the question above, if you tripled the slant height and radius of a cone, the formula to find the modified surface area of the cone would be 6 and 6.

I hope my answer helped you. Have a nice day!