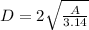Question

The area (A) of a circle with a radius of r is given by the formula A=3.14r^2 and its diameter (d) is given by d=2r. Arrange the equations in the correct sequence to rewrite the formula for diameter in terms of the area of the circle.

Answer 1

`D=2\sqrt{(A)/(3.14)}`

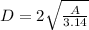
Explanation:

we know that

The area of a circle is

`A=3.14r^(2)` ----> equation A

The diameter of a circle is

`D=2r` ----> equation B

Solve for r in the equation A

That means ---> isolate the variable r

Divide by 3.14 both sides

`(A)/(3.14)=r^(2)`

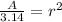
take the square root both sides

`\sqrt{(A)/(3.14)}=r`

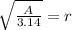
Rewrite

`r=\sqrt{(A)/(3.14)}`

Substitute the value of r in the equation B

`D=2\sqrt{(A)/(3.14)}`