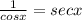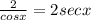Question

Verify the identity.

cosine of x divided by quantity one plus sine of x plus quantity one plus sine of x divided by cosine of x equals two times secant of x.

Answer 1

For the answer to the question above,
cosx/(1+sinx) + (1+sinx)/cosx
= (cosx * cosx + (1+sinx)(1+sinx)) / (cosx (1+sinx))
= (cos²x + sin²x + 2 sinx + 1) / (cosx (1+sinx))
= (1 + 2 sinx + 1) / (cosx (1+sinx))
= (2 + 2 sinx) / (cosx (1+sinx))
= 2 (1+sinx) / (cosx (1+sinx))
= 2/cosx
= 2 secx
I hope my answer helped you. Have a nice day!

Answer 2

We have been given an expression

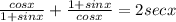`(cosx)/(1+sinx)+(1+sin x)/(cosx)=2sec x` (1)

We have to verify equation (1)

We will pick the left hand side of the equation and prove it to right hand side

Taking LCM on LHS of the equation (1) we get

`(cos^2x+(1+sinx)^2)/((1+sinx)(cosx))`

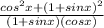
Now open the parenthesis and simplify we get

`(cos^2 x+1+sin^2 x+2sinx)/(cosx(1+sinx))`

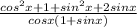
since,
`cos^2x+sin^2x=1`

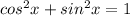
Now, further simplify we get

`(2+2sinx)/(cosx(1+sinx))=(2(1+sinx))/(cosx(1+sinx))`

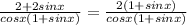
Cancel the common factor which is (1+sinx) we get

`(2)/(cosx)`

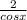
Since,
`(1)/(cosx)=secx`

`(2)/(cosx)=2secx`