Answer:
The answer is
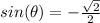

Explanation:
we know that

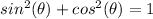
In this problem we have
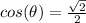
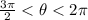
so
The angle
 belong to the third or fourth quadrant
belong to the third or fourth quadrant
The value of
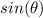 is negative
is negative
Step 1
Find the value of
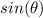
Remember
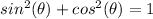
we have
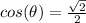
substitute
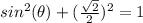
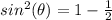
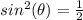
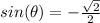 ------> remember that the value is negative
------> remember that the value is negative
Step 2
Find the value of
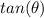

we have
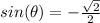
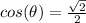
substitute

