Question

In a sample of 200 households, the mean number of hours spent on social networking sites during the month of January was 55 hours. In a much larger study, the standard deviation was determined to be 7 hours. Assume the population standard deviation is the same. What is the 99% confidence interval for the mean hours devoted to social networking in January?

Answer 1

53.7279 ≤ μ ≤ 56.2721

Explanation:

If the mean of the sample is known, the population standard deviation is known and the size of the sample is bigger than 30, the (1-∝) confidence interval is calculated as:

`x-z_(\alpha/2)*(s)/(√(n))` ≤ μ ≤
`x+z_(\alpha/2)*(s)/(√(n))`

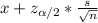
Where x is the mean of the sample, s is the population standard deviation, n is the size of the sample and
`z_(\alpha/2)` is the value of the standard normal distribution in which:

P(Z>z)=∝/2

If 1-∝ is equal to 99%, ∝/2 is equal to 0.005 and
`z_(\alpha/2)` is equal to 2.57

So, if we replace x by 55, s by 7, n by 200 and
`z_(\alpha/2)` by 2.57, we get:

`55-2.57*(7)/(√(200))` ≤ μ ≤
`55+2.57*(7)/(√(200))`

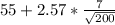
55 - 1.2721 ≤ μ ≤ 55 + 1.2721

53.7279 ≤ μ ≤ 56.2721