Question

A barrel of tomato sauce has spilled on a tile floor. The sauce flow can be expressed with the function r(t) = 2t, where t represents time in minutes and r represents how far the sauce is spreading.

The spilled sauce is creating a circular pattern on the tile. The area of the pattern can be expressed as A(r) = πr2.

Part A: Find the area of the circle of spilled sauce as a function of time, or A[r(t)]. Show your work. (6 points)

Part B: How large is the area of spilled sauce after 5 minutes? You may use 3.14 to approximate π in this problem. (4 points)

Answer 1

As per the statement:

The sauce flow can be expressed with the function is given by:

`r(t) = 2t`

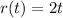
where, t represents time in minutes and r represents how far the sauce is spreading.

The spilled sauce is creating a circular pattern on the tile.

The area of the pattern can be expressed as:

`A(r) = \pi r^2`

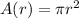
Part A.

To find the area of the circle of spilled sauce as a function of time.

`A[r(t)]`

then;

`A[r(t)] = \pi (r(t))^2`

Substitute the function r(t) we have;

`A[r(t)] = \pi (2t)^2 = \pi 4t^2 = 4 \pi t^2` .....[1]

therefore, the area of the circle of spilled sauce as a function of time, is:

`A[r(t)] = 4 \pi t^2`.

Part B:

We have to find how large is the area of spilled sauce after 5 minute.

use π = 3.14 and t = 5 minutes

Substitutes these in [1] we have;

`A[r(5)] = 4 \cdot 3.14 \cdot 5^2`

⇒
`A[r(5)] = 100 \cdot 3.14`

Simplify:

`A[r(5)] = 314` square unit

therefore, 314 square unit large is the area of spilled sauce after 5 minute.

Answer 2

For the answer to the question above, I'll show my solution for the answer below.
Area A = pi r^2
The rate of change of area = d A/ d t = 2 pi r d r/d t
r= 2t, d r = 2 d t
This gives
d A/ d t = 2 pi 2t 2 d t = 8 pi t dt
Integrate it
A= 4 pi t^2.
After t=5, the area will be 100* 3.14 square= 314 square units.