Question

Using the conversion factor from eV (electron volts) to joules, determine which energy line for an electron dropping from one energy level to another would show a line at 435 nm in an emission spectrum. Use the formulas and the energy level information below to answer the question.

Needed constants:

1.00eV = 1.6 * 10^-19 J
c = 3.00 * 10^8 m/s
h = 6.63 * 10^-34 J*s

Energy Level Values:
E6: E= -0.378 eV
E5: E= -0.544 eV
E4: E= -0.850 eV
E3: E= -1.51 eV
E2: E= -3.403V

Answer 1

The formula used to solve this is:
E = hc/λ

The given values can then be subsituted into the equation to sovle for the energy:

E = (6.63 x 10^-34 J-s) (3 x 10^8 m/s) / 435 x10^-9 m
E = 4.5724 x 10^-19 J

converting to electron volts
E = 4.5724 x 10^-19 J * 1.00eV / 1.6 * 10^-19 J
E = 2.86 eV

The closest energy line is
E2

Answer 2

Step-by-step explanation:

Wavelength in an emission spectrum,
`\lambda=435\ nm=435* 10^(-9)\ m`

The energy of an electron is given by :

`E=(hc)/(\lambda)`

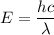
Where

h is the Planck's constant

c is the speed of light

For 435 nm, the energy of the electron will be :

`E=(6.63* 10^(-34)* 3* 10^8\ m/s)/(435* 10^(-9))`

`E=4.57* 10^(-19)\ J`

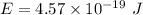
We know that
`1\ eV=1.6* 10^(-19)\ J`

So,
`E=(4.57* 10^(-19))/(1.6* 10^(-19))`

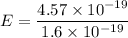
So, E = 2.86 eV

The energy of the electron dropping from one energy level is 2.86 eV. We know that,

`(hc)/(\lambda)=E_(n_2)-E_(n_1)`

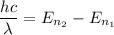
From the given energy levels :

`E_5-E_2=-0.544-(-3.403)`

`E_5-E_2=2.859\ eV`

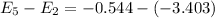
So, the transition must be from E₅ to E₂. Hence, this is the required solution.