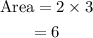Given:
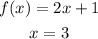
Parallel line slope are also same then parallel line equation is:
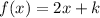
The line pass (2,7) then:
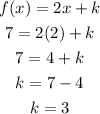
So two parallel line equation is :
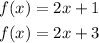
As the difference in y intrcepts is 2.
The side of parallelogram along y- axis is 2.
Two other parallel line are x=0 and x=3
so vertical distance between them is 3
so area is: