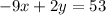Question

A line passes through (-7,-5) and (-5,4). Write an equation for the line in point-slope form. Rewrite the equation in standard form using integers.

A. y+5= 9/2 (x-7); -9x+2y=53
B. y+7= 9/2 (x+5); -9x+2y=31
C. y+5= 9/2 (x+7); -9x+2y=53
D. y-5= 9/2 (x+7); -9x + 2y=-53

Answer 1

Option C is correct

`y+5 = (9)/(2)(x+7)`

`-9x+2y=53`

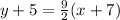
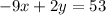
Explanation:

Point slope form:

The equation of line is given by:

`y-y_1=m(x-x_1)` ....[1] where m is the slope and a point
`(x_1, y_1)` lies on the line.

Given that:

A line passes through (-7,-5) and (-5,4).

Calculate slope:

Slope is given by:

`\text{Slope} = (y_2-y_1)/(x_2-x_1)`

Substitute the given values we have;

`\text{Slope (m)} = (4-(-5))/(-5-(-7))`

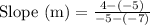
Simplify:

`m = (9)/(2)`

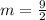
Substitute thee value of m and (-7, -5) in [1] we have;

`y-(-5)=(9)/(2)(x-(-7))`

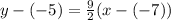
Simplify:

`y+5 = (9)/(2)(x+7)`

⇒
`2(y+5) = 9(x+7)`

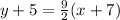
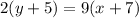
Using distributive property :
`a \cdot(b+c) = a\cdot b+ a\cdot c`

`2y+10=9x+63`

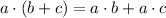
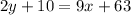
Subtract 9x from both sides we have;

`-9x+2y+10=63`

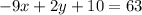
Subtract 10 from both sides we have;

`-9x+2y=53`

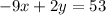
Therefore, an equation for the line in point-slope form is
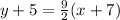`y+5 = (9)/(2)(x+7)` and the equation in standard form using integers is
`-9x+2y=53`

Answer 2

The equation:
y - y 1 = ( y2 - y1 ) / ( x2- x1) * ( x - x1 )
y - ( - 5 ) = ( 4 + 5 ) / ( - 5 + 7 ) * ( x - ( - 7 ) )
y + 5 = 9/2 ( x + 7 )
y + 5 = 9/2 x + 63 /2 / * 2
2 y + 10 = 9 x + 63
- 9 x + 2 x = 53
Answer:
C ) y + 5 = 9/2 ( x + 7 ) ; - 9 x + 2 y = 53