Question

The equation x^2+y^2-4x+2y=b describes a circle. Determine the y-coordinate of the center of the circle.

The radius of the circle is 7 units. What is the value of b in the equation?

Answer 1

x² + y² - 4 x + 2 y = b
x² - 4 x + 4 + y² + 2 y + 1 = b + 4 + 1
( x - 2 )² + ( y + 1 )² = b + 5
y - coordinate of the center of the circle is: y = - 1
b + 5 = r
b + 5 = 7
b = 7 - 5
b = 2

Answer 2

Explanation:

The equation is given as:

`x^2+y^2-4x+2y=b`

Upon solving this equation, we have

`x^2-4x+4+y^2+2y+1=b+4+1`

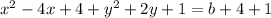
which can be written as:

`(x-2)^2+(y+1)^2=b+5` (1)

Thus, the y- coordinate of the center of the circle is
`y=-1`.

Now, comparing the equation (1) with the equation of circle, we have

`(x-a)^2+(y-c)^2=r^2`

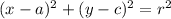
where r is the radius of the circle and (a,c) is the center.

Thus, on comparing, we have

⇒
`b+5=r^2`

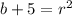
Also, it is given that the radius of the circle is 7 units, thus putting r=7 in above equation, we get

⇒
`b+5=(7)^2`

⇒
`b+5=49`

⇒
`b=44 units`

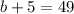
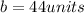
Thus, the value of b is 44 units in the given equation.