Given:
4 types of crust
6 types of toppings
7 kinds of cheese
Find the number of different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese.
Solution:
In choosing a crust, there are only 4 ways to choose since there are only 4 options.
In choosing 3 different toppings out of 6, we can use the combination formula since the order doesn't matter. The formula is:
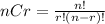
in which n = 6 and r = 3.
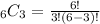
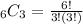
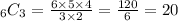
Hence, there are 20 different combinations of three toppings we can form out of 6 available toppings.
Lastly, in choosing 2 kinds of cheese out of 7, we can still use the combination formula in which n = 7 and r = 2.
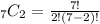
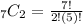
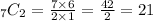
Hence, there are 21 combinations of 2 kinds of cheese from the 7 available types of cheese.
So, the number of different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese is:
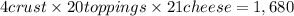
There are 1, 680 different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese.