Question

Paolo's Pizzeria offers 4 types of crust, 6 toppings, and 7 kinds of cheese for the mega calzone. How many different mega calzones can be made if a mega calzone contains 3 different toppings and 2 different cheeses?

Answer 1

Given:

4 types of crust

6 types of toppings

7 kinds of cheese

Find the number of different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese.

Solution:

In choosing a crust, there are only 4 ways to choose since there are only 4 options.

In choosing 3 different toppings out of 6, we can use the combination formula since the order doesn't matter. The formula is:

`nCr=(n!)/(r!(n-r)!)`

in which n = 6 and r = 3.

`_6C_3=(6!)/(3!(6-3)!)`
`_6C_3=(6!)/(3!(3!))`
`_6C_3=(6*5*4)/(3*2)=(120)/(6)=20`

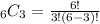
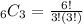
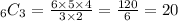
Hence, there are 20 different combinations of three toppings we can form out of 6 available toppings.

Lastly, in choosing 2 kinds of cheese out of 7, we can still use the combination formula in which n = 7 and r = 2.

`_7C_2=(7!)/(2!(7-2)!)`
`_7C_2=(7!)/(2!(5)!)`
`_7C_2=(7*6)/(2*1)=(42)/(2)=21`

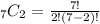
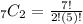
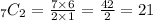
Hence, there are 21 combinations of 2 kinds of cheese from the 7 available types of cheese.

So, the number of different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese is:

`4crust*20toppings*21cheese=1,680`

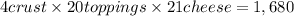
There are 1, 680 different mega calzones that can be made with 3 different toppings and 2 different kinds of cheese.