Question

A polynomial function has a root of –6 with multiplicity 1, a root of –2 with multiplicity 3, a root of 0 with multiplicity 2, and a root of 4 with multiplicity 3. If the function has a positive leading coefficient and is of odd degree, which statement about the graph is true?

The graph of the function is positive on (–6, –2).

The graph of the function is negative on (-infinity, 0).

The graph of the function is positive on (–2, 4).

The graph of the function is negative on (4, infinity).

Answer 1

A. The graph of the function is positive on (–6, –2).

Explanation

Cause Yeet 8D

Answer 2

The right answer is: The graph of the function is positive on (–6, –2)

So let's write in mathematical language each statement to solve this problem:

1. A polynomial function has a root of –6 with multiplicity 1

This can be written like this:

`(x+6)`

2. It has a root of –2 with multiplicity 3

Writing this statement as follows:

`(x+2)^3`

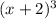
3. It has a root of 0 with multiplicity 2

So, this statement is:

`x^2`

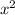
4. and it has a root of 4 with multiplicity 3

`(x-4)^3`

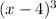
So, groping all these terms we have:

`f(x)=x^2(x+6)(x+2)^3(x-4)^3`

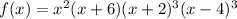
Moreover, the last statement says that the function has a positive leading coefficient and is of odd degree, say, this coefficient is 9, then the complete polynomial function is:

`f(x)=9x^2(x+6)(x+2)^3(x-4)^3`

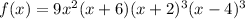
From the Figure below you can see that the only right statement is that the graph of the function is positive on (–6, –2)