Answer:
Domain of validity--
All real numbers except nπ where n belongs to integers.
( Since,
 )
)
Explanation:
We are asked to prove the trignometric identity:
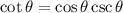
We know that the cotangent function is given by the formula:
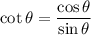
Also we know that:
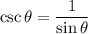
Hence, we have:
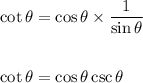
Now, the domain of validity i.e. the values for which the cotangent function is defined is the set of all the real number except where sine function is zero.
Since the sine function appear in the denominator and for a function to be well defined denominator term must be non-zero.