Refer to the image attached.
Given:
 and
and
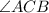 are congruent.
are congruent.
To Prove:
 ABC is an isosceles triangle.
ABC is an isosceles triangle.
Construction: Construct a perpendicular bisector from point B to Line segment AC.
Consider triangle ABD and BDC,
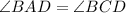 (given)
(given)
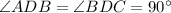
(By the definition of a perpendicular bisector)
 (By the definition of a perpendicular bisector)
(By the definition of a perpendicular bisector)
Therefore,
 by Angle Side Angle(ASA) Postulate.
by Angle Side Angle(ASA) Postulate.
Line segment AB is congruent to Line segment BC because corresponding parts of congruent triangles are congruent.(CPCTC)