Question

Suppose a countrys population in 1980 was 210 million. In 1990 it was 225 million. Using the exponential growth formula, P=Ae^kt, estimate the countrys population in 2000

Answer 1

The countries population in 2000 was 241,08 millions

Explanation:

To resolve this exercise we need to know the exponential model:

`P_(_t_)=P_0*e^k^t`

Where:

`P_(_t_)`: The population in certain time

`P_(_0_)`: Initial population

k: constant

t: time frame

With the problem information we can find the constant (k), because we have all the information in t=10 years (1990-1980=10 years)

`P_(_1_9_9_0_)=P_(_1_9_8_0_)*e^k^1^0`

`225m=210*e^1^0^k`

`(225m)/(210m)=e^1^0^k`

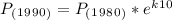
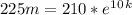
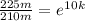
We multiply by natural logarithm on both sides of this equation and we have:

`Ln((15m)/(14m))=10*k\\k=(Ln(15)/(14))/(10)\\k=0.0069`

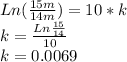
With the constant (k) we can find the population in 2000

`P_(_0_)=210m`: Initial population

k=0.0069

t=20 years (2000-1980=20 years)

`P_(_2_0_0_0_)=P_(_1_9_8_0_)*e^k^2^0`

`P_(_2_0_0_0_)=210m*e^0^.^0^0^6^9^*^2^0`

`P_(_2_0_0_0_)=210m*e^0^.^1^3^8`

`P_(_2_0_0_0_)=210m*1.1479`

`P_(_2_0_0_0_)=241.08m`

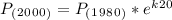
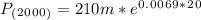
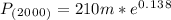
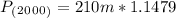
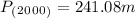
The countries population in 2000 was 241,08 millions

Answer 2

P=Ae^kt
225 = 210 * e^(k*(1990-1980)
225/210=e^10k ln(225/210)=10k
k=ln(225/210)/10=0.0069
P = 210*e^(0.0069t)
for 2000 ===> t = 2000-1980=20
P = 210*e^(0.0069*20)
P=241.0749=241