Question

With one method of a procedure called acceptance sampling, a sample of items is randomly selected without replacement and the entire batch is accepted if every item in the sample is okay. A company just manufactured 796 CDs, and 205 are defective. If 3 of these CDs are randomly selected for testing, what is the probability that the entire batch will be accepted?

Answer 1

Answer: 0.405224

Explanation:

Given : A company just manufactured 796 CDs, and 205 are defective.

Then, the probability that a CD is defective :
`p=(205)/(796)=0.257537688442\approx0.26`

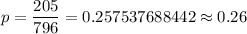
Sample size : n= 3

Binomial probability formula :

`P(x)=^nC_xp^x(1-p)^(n-x)`

By using binomial probability formula, the probability that none 3 CDs is defective:-

`P(3)=^3C_3(0.26)^0(1-0.26)^(3)\\\\=(1)(0.74)^3\ \ [\text{Since}^nC_n=1]\\\\=0.405224`

Hence, the the probability that the entire batch will be accepted= 0.405224

Answer 2

The probability that the first CD in the sample is not defective is 591/796 The probability that the second CD in the sample is not defective is 590/795 The probability that the third CD in the sample is not defective is 589/794

P(sample has 0 defective CDs)=591×590× 589796×795×794=
you can calculate