Solution
Firstly, we need to find the equation of the line passing through the points
W(1, 3) and X(2, 6)
and also the equation of the line passing through the points Y(4, 4), and Z(7, 3)
The line WX is given as
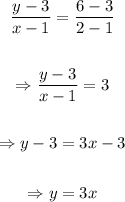
The line YZ is given as
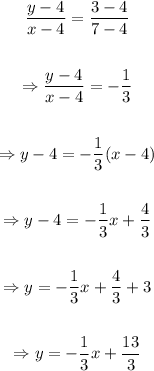
The gradient of WX is 3
The gradient of YZ is -1/3
Since the product of the gradient WX and YZ

Hence WX is perpendicular to YZ