Question

For an angle Θ with the point (12, −5) on its terminating side, what is the value of cosine?

Answer 1

The value of cosine is
`(12)/(13)`.

Explanation:

It is given that an angle
`{\theta}`, with the point (12,-5) is on its terminating side, then the adjacent sides has measure =12 and the opposite side has measure =-5.

Now, from the figure drawn, using the Pythagoras theorem, we have

`(Hyp)^2=(Base)^2+(Per)^2`

⇒
`(H)^2=(12)^2+(-5)^2`

⇒
`(H)^2=144+25`

⇒
`(H)^2=169`

⇒
`H=13`

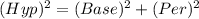
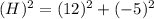
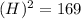
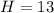
Thus, the value of hypotenuse is 13units.

Now, the value of cosine is given as:

`cosine=(adjacent)/(hypotenuse)`

⇒
`cosine=(12)/(13)`

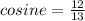
Therefore, the value of cosine is
`(12)/(13)`.

Answer 2

Well, in order to answer this problem we need to use the the Pythagorean Theorem and the it will be like this:
cos = x / hypotenuse
cos= 12/13
I think with this you can figure the rest out. Hope this helps