Question

How does the graph of

f(x)=3(4)^x-5+2/3
relate to its parent function?
I am struggling with this question and honestly don't know how to do it. Any input on the possible answers?

*Please select all correct answers*
A- The parent function has been translated to the right.

B- The parent function has been compressed.

C- The parent function has been translated up.

D- The parent function has been stretched.

Answer 1

A,C,&D

Explanation:

Answer 2

A,C and D

Explanation:

We are given that

`f(x)=3(4)^(x-5)+(2)/(3)`

We have to find the graph of given function relate to its parent function.

Let parent function

`g(x)=4^x`

Now, the graph shift 5 unit towards right by the rule of transformation

`g(x)\rightarrow g(x-5)`

Therefore, by using this rule then, we get

`g(x)=(4)^(x-5)`

Now, stretch vertically 3 times the previous graph by using the rule of transformation

`f(x)\rightarrow 3f(x)`

Now, after applying this rule we get

`g(x)=3(4)^(x-5 )`

Now, shift the graph
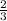`(2)/(3)` unit upward by the rule of transformation

`f(x)\rightarrow f(x)+(2)/(3)`

After applying this rule then, we get

`f(x)=3(4)^(x-5)+(2)/(3)`

Hence, options A ,C and D are true.