The independent variable is
X: age of best actress winner
The dependent variable is
Y: age of best actor winner
1) First you have to determine the regression equation.
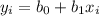
b₀ is the estimate of the y-intercept
b₁ is the estimate of the slope
To calculate b₁ you have to use the following formula
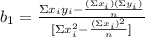
As you can see in this formula you need to calculate the sums of the observed data for each variable
For this sample of n=12 actors and actresses
Σx=473
Σx²=20883
Σy=544
Σy²=25436
Σxy=21064
Replace the calculations in the formula:
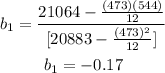
The slope of the regression line is b₁=-0.17
Next is to calculate the y-intercept of the regression equation, to do so you need to use the following formula:
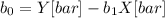
Y[bar] is the average age of the actors
X[bar] is the average age of the actresses
Calculate the average values for each variable:


And now we can calculate the y-intercept
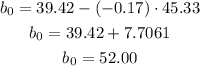
The y-intercept of the regression equation is b₀= 52.00 years
So the regression equation for the age of the actors that won the best actor award in regards of the age of the actresses that won the best actress award is
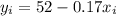
2)
Using the calculated regression equation you can estimate the age of the male winner for a certain age of the female winer.
If the best actress that year was x=32 years old, replace that value in the formula to determine the age of the best actor winner
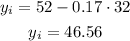
The estimated age for the best actor winner is 46.56 years, when the best actress winner is 32 years old.
3)If the age of the actual winner is 49 years old, calculate the difference between the actual value and the estimated value to determine if the estimation is within 5 years of the observed value
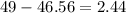
The estimated age is within 5 years of the actual age of the best actor winner.