Question

1) Find the regression equation, letting the first variable be the predictor (x) variable. 2) Using the listed actress/actor ages in various years, find the best predicted age of the Best Actor winner given that the age of the Best Actress winner that year is 32 years. 3) Is the result within 5 years of the actual Best Actor winner, whose age was 49 years? Best Actress 27 32 28 64 33 32 46 28 61 22 46 54 Best Actor 44 39 36 43 48 49 62 53 40 54 44 32 Find the equation of the regression line. y=0+ ( )x (Round the constant to one decimal place as needed. Round the coefficient to three decimal places as needed.)

Answer 1

The independent variable is

X: age of best actress winner

The dependent variable is

Y: age of best actor winner

1) First you have to determine the regression equation.

`y_i=b_0+b_1x_i`

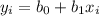
b₀ is the estimate of the y-intercept

b₁ is the estimate of the slope

To calculate b₁ you have to use the following formula

`b_1=(\Sigma x_iy_i-((\Sigma x_i)(\Sigma y_i))/(n))/(\lbrack\Sigma x^2_i-((\Sigma x_i)^2)/(n)\rbrack)`

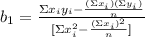
As you can see in this formula you need to calculate the sums of the observed data for each variable

For this sample of n=12 actors and actresses

Σx=473

Σx²=20883

Σy=544

Σy²=25436

Σxy=21064

Replace the calculations in the formula:

`\begin{gathered} b_1=(21064-((473)(544))/(12))/(\lbrack20883-((473)^2)/(12)\rbrack) \\ b_1=-0.17 \end{gathered}`

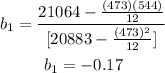
The slope of the regression line is b₁=-0.17

Next is to calculate the y-intercept of the regression equation, to do so you need to use the following formula:

`b_0=Y\lbrack bar\rbrack-b_1X\lbrack bar\rbrack`

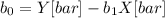
Y[bar] is the average age of the actors

X[bar] is the average age of the actresses

Calculate the average values for each variable:

`\begin{gathered} Y\lbrack bar\rbrack=(\Sigma y_i)/(n) \\ Y\lbrack bar\rbrack=(473)/(12) \\ Y\lbrack bar\rbrack=39.42 \end{gathered}`
`\begin{gathered} X\lbrack bar\rbrack=(\Sigma x_i)/(n) \\ X\lbrack bar\rbrack=\frac{544_{}}{12} \\ X\lbrack bar\rbrack=45.33 \end{gathered}`

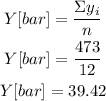
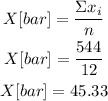
And now we can calculate the y-intercept

`\begin{gathered} b_0=39.42-(-0.17)\cdot45.33 \\ b_0=39.42+7.7061 \\ b_0=52.00 \end{gathered}`

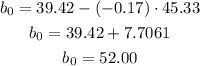
The y-intercept of the regression equation is b₀= 52.00 years

So the regression equation for the age of the actors that won the best actor award in regards of the age of the actresses that won the best actress award is

`y_i=52-0.17x_i`

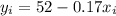
2)

Using the calculated regression equation you can estimate the age of the male winner for a certain age of the female winer.

If the best actress that year was x=32 years old, replace that value in the formula to determine the age of the best actor winner

`\begin{gathered} y_i=52-0.17\cdot32 \\ y_i=46.56 \end{gathered}`

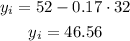
The estimated age for the best actor winner is 46.56 years, when the best actress winner is 32 years old.

3)If the age of the actual winner is 49 years old, calculate the difference between the actual value and the estimated value to determine if the estimation is within 5 years of the observed value

`49-46.56=2.44`

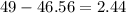
The estimated age is within 5 years of the actual age of the best actor winner.