Given that the probability of dying is 0.003852, the probability of living will be
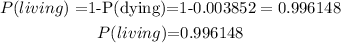
Annual insurance charge=387.
Thus, the gain or loss from death will be
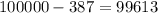
The gain or loss from when alive will be -387, since she does not get the death benefit when alive instead she pays the annual insurance charge.
Thus, the Expected value of insurance policy is evaluated as
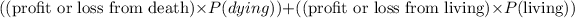
This is calculated to be
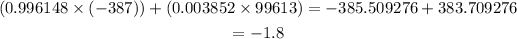
Thus, the expected value is $ 1.8