Question

A two-way frequency table shows grades for students in college and students in high school.

Based on this data, are "being in high school" and "GPA above 3.0" independent events?
Yes, P(high school | GPA above 3.0) = P(high school)

Yes, P(high school | GPA above 3.0) = P(GPA above 3.0)

No, P(high school | GPA above 3.0) ≠ P(high school)

No, P(high school | GPA above 3.0) ≠ P(GPA above 3.0)

Answer 1

If two events A and B are independent, then P(A | B) = P(A)

P(high school | GPA above 3.0) = 14/40 = 0.35
P(high school) = 60/100 = 0.6

Therefore, the two events are not independent because P(high school | GPA above 3.0) ≠ P(high school)

Answer 2

Answer: No, P(high school | GPA above 3.0) ≠ P(high school)

Explanation:

Since we have given that

A two-way frequency table.

We need to show that "being in High School (H)" and "GPA above 3.0 (G)" are independent events:

So, for independent events we need to show that

`P(H\mid G)=P(H)`

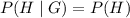
First we will calculate the "Conditional probability" :

`P(H\mid G)=(14)/(40)=0.35`

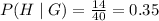
And Probability of getting "Being in High school ":

`(60)/(100)\\\\=0.6`

And we get that

`P(H\mid G)\\eq P(H)`

Hence, They are not independent events.

No, P(high school | GPA above 3.0) ≠ P(high school)