Question

For questions 1 and 2, use the diagram below.

1. The figure above is a regular octagon with radii and an apothem drawn. What is the measure of angle 1?
A. 22.5 degrees
B. 45 degrees
C. 60 degrees
D. 67.5 degrees

2. What is the measure of angle 2?
A. 22.5 degrees
B. 45 degrees
C. 60 degrees
D. 67 degrees

Answer 1

1) it's just 360 divided by 8 sectors = 45 degrees (answer B)
2) (180-45)/2 = 67.50 (answer D is the nearest)

Answer 2

Answer: The correct options are (1). B, (2). D.

Step-by-step explanation: We are given a figure with a regular octagon where the radius and an apothem are drawn.

(1) We are to find the measure of ∠1.

The radius of the regular octagon divides it into 8 congruent isosceles triangles, where the sum of the vertex angles of each of the triangles is 360°.

If, 'β' denotes the measure of each vertex angle, then we must have

`8\beta=360^\circ\\\\\Rightarrow \beta=(360^\circ)/(8)\\\\\Rightarrow \beta=45^\circ.`

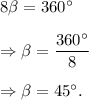
Since ∠1 is also a vertex angle of one of the isosceles triangles.

Therefore,

m∠1 = β

⇒m∠1 = 45°.

Thus, option (B) is correct.

(2) We are to find the measure of ∠2.

The measures of the two base angles opposite to the equal sides of an isosceles triangle are equal.

So, from the isosceles triangle with one of the base angles as ∠2 that

`45^\circ+m\angle 2+m\angle 2=180^\circ\\\\\Rightarrow 45^\circ+2* m\angle 2=180^\circ\\\\\Rightarrow 2* m\angle 2=135^\circ\\\\\Rightarrow m\angle 2=67.5^\circ.`

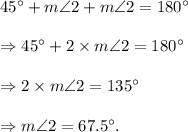
Thus, option (D) is correct.

The correct options are (1). B, (2). D.