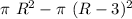Question

Question: "In the figure below, both circles have the same center, and the radius of the larger circle is R. If the radius of the smaller circle is 3 units less than R, which of the following represents the area of the shaded region?"

Answer IS: (pi)R^2-(pi)(R-3)^2
*Can someone explain how? I don't even know how to start. ~will draw diagram under~

Answer 1

The formula for the area of a circle is πr^2, where r is the radius of the circle.
The area of your figure is (outer circle)-(inner circle)
plugging in R and R-3 for radii:
the area of the shaded region is (pi)R^2-(pi)(R-3)^2
hope this helped!

Answer 2

Answer:
`\pi\ R^2-\pi\ (R-3)^2`

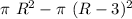
Explanation:

Given : Two circles centered at the same center

Radius of the larger circle = R units

Radius of smaller circle= R-3 units

We know that area of circle with radius 'r' is
`\pi\ r^2`

Area of the larger circle=
`\pi\ R^2`

Area of the smaller circle =
`\pi\ (R-3)^2`

Therefore, the area of the shaded region

=Area of the larger circle-Area of the smaller circle

=
`\pi\ R^2-\pi\ (R-3)^2`