Question

Compare the y-intercepts and the rates of change of the following items.

The items have different y-intercepts and different rates of change.

The rates of change are the same, but the y-intercepts are different.

The y-intercepts are the same, but the rates of change are different.

The items have the same y-intercept and the same rate of change.

Answer 1

The y-intercept denotes where a line crosses the y-axis, and the slope or rate of change indicates how steep the line is. Differing y-intercepts and slopes result in lines crossing the y-axis at different points and having different angles, whereas equal values mean lines are either parallel or identical.

Step-by-step explanation:

The student's question pertains to comparing the y-intercepts and rates of change of linear equations, which are fundamental concepts in algebra. When talking about linear equations, the rate of change is another term for the slope of the line, often represented by the variable 'm'. The y-intercept is the value 'b' and indicates where the line crosses the y-axis. Now, let's delve into the comparisons.

• For items with different y-intercepts and different rates of change, the lines cross the y-axis at different points and also have different angles in relation to the x-axis.
• When the rates of change are the same but the y-intercepts are different, the lines are parallel to each other and only differ in vertical position.
• If the y-intercepts are the same but the rates of change vary, it means the lines start from the same point on the y-axis but then diverge because they have different slopes.
• For lines with the same y-intercept and the same rate of change, they are completely superimposed on each other as they have the same starting point and increase at the same rate.

An example provided is the line with a y-intercept of 9 and a slope of 3. This tells us that the line will cross the y-axis at 9, and for every 1 unit increase in x, the value of y will increase by 3 units.

Answer 2

Answer: The correct option is

(C) The y-intercepts are the same, but the rates of change are different.

Step-by-step explanation: We are given to compare the y-intercepts and the rates of change of the given items.

For item I :

The given equation of the line is in slope-intercept for, as follows :

`y=2x-4.`

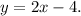
So, the y-intercept of the line is -4 and the rate of change is given by the slope of the line, i.e., 2.

For item II :

We see that

at x = 0, the value of y is -4. So, the y-intercept of the linear function (a line) is -4.

Now, (-4, -6) and (-2, -5) are two points on the line, so the rate of change will be

`R=(-5-(-6))/(-2-(-4))=(1)/(2).`

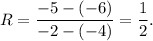
Therefore, the y-intercepts are same but rate of changes are different.

Thus, (C) is the correct option.