Question

Which of the following shows the correct work and solution to the exponential equation 5x - 1=25

Answer 1

We have the expression:

`5^(x-1)=25`

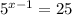
And we need to solve this for x.

Let's solve this expression and then see which of the options is the correct one.

The first step to solve this is that we need for the two sides of the equation to have the same base. (the number 5 on the left side is the base, so we need to also have a 5 as the base on the right side).

We do this by noting that:

`25=5^2`

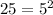
We know that 25 is equal to 5 squared (because 5x5 is 25)

So the first step is to substitute 25 for 5 squared:

`5^(x-1)=5^2`

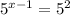
Since we have the same base on both sides (5), we follow the rule:

• If we have the same base on both sides of an equation, the exponents have to be equal

Thus, the second step to solve is to equal the exponents:

`x-1=2`

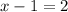
Finally, to solve this equation for x, we just need to add 1 to both sides to get rid of the -1 on the left side:

`\begin{gathered} x-1+1=x=2+1 \\ \end{gathered}`

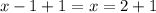
And the third step is:

`x=3`

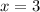
As we can see, these three steps are represented in the third option In which we get the same result of x=3.

Answer: x=3