Question

"Using the graph as your guide, complete the following statement.

The discriminant of the function is _____.

Answer 1

Answer: zero

Explanation:

Answer 2

Option B is correct

The discriminant of the function is Zero

Explanation:

Using the definition of quadratic equation:

The root of the equation can be found using the formula:

`x = (-b \pm √(b^2-4ac))/(2a)`

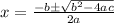
The discriminant(D) in the given formula is:

`D = b^2-4ac`

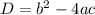
We have to find the discriminant of the given function.

There are following 3 cases.

Case 1.

If D > 0

then there are two real solutions.

Case 2.

If D < 0

then;

there are no real solutions.

Case 3:

If D = 0

then;

there is a real solution with multiplicity 2.

In the given graph:

You can see that the graph of the quadratic equation touches the x-axis at (5, 0)

Then;

there is a real solution with multiplicity of 2.

Therefore, The discriminant of the function is, zero