In order to determine the points of intersection proceed as follow:
Equal both equations:
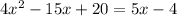
Write the previous equation as an standard quadratic equation:
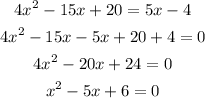
to obtain the last equation you divide by 4 both sides.
Now, use the quadratic formula, with a = 1, b = -5 and c = 6, to find the solution for x:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
![\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(1)(6)}}{2(1)} \\ x=\frac{5\pm\sqrt[]{25-24}}{2} \\ x=(5\pm1)/(2) \\ x_1=(5-1)/(2)=(4)/(2)=2 \\ x_2=(5+1)/(2)=(6)/(2)=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/z5bmqdvi9oqtet30fbug.png)
The previous solutions mean that for the values of x = 2 and x = 3 the given functions intersect each other.
By replacing the values of x into any of the functions, for instance, in
y = 5x - 4, you get:
y = 5(2) - 4 = 10 - 4 = 6
y = 5(3) - 4 = 15 - 4 = 11
Then, the points of intersection are:
(2 , 6)
(3 , 11)
The graph is shown below: