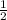Answer:
Explanation:
This is due to radical to exponent change property which is
![\sqrt[n]{x}=x^{(1)/(n)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/nea0q1gj8xsshu9b8gmieu2s56a4xbo6rx.png)
We can consider some examples as below;
![\sqrt[3]{4}=4^{(1)/(3)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/lg2hwuem6os2t3ab83vt3jr5cs828ms5ge.png)
![\sqrt[2]{5}=5^{(1)/(2)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/pqxwfshbycsq0kqtzyhj3th60hkwh8g8jj.png)
Hence, the square root of a number is defined to be equal to that number to the
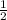 power.
power.
Or we sometimes solve square root by taking the power as