It's important to know that the domain refers to the x-values of the function, and the range refers to the y-values of the function. Graphically, the domain would be the x-axis and the range would be the y-axis, that is, their values.
As you can observe in the given graph, the function doesn't have any interruption or restriction horizontally, it goes from the negative x-axis to the positive x-axis, this means the domain is all real numbers from negative infinity to positive infinity, as follows
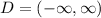
On the other hand, the range of the given function is from y = -2 to positive infinity, it's important to know that y = -2 is excluded from the range because as you can observe the function curves there without crossing y = -2. So, the range is
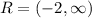
For the second question of the problem, we have to select two y-values from x = 0 and x = 1, which is the given interval. From the graph, we can identify that x = 0 belongs to y = -1, and x = 1 belongs to y = 1. So, we have the points (0,-1) and (1,1). Now, we use the following formula to find the average rate of change.
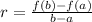
Where a = 0, f(a) = -1, b = 1, and f(b) = 1, note that these values are the coordinates of the two points we selected. Let's use these values to find the rate.
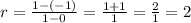
Therefore, the average rate of change over the interval [1,0] is 2.