Given:
The equation is
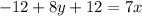
To find:
The constant of direct variation if the given equation represents direct variation.
Solution:
If y is directly proportional to x, then
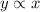
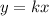 ...(i)
...(i)
Where, k is the constant of proportionality.
We have,
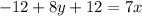
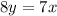
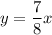 ...(ii)
...(ii)
At x=0,
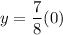

The equation (ii) passes through (0,0). So, it represents a proportional relationship.
On comparing (i) and (ii), we get
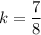
Therefore, the constant of proportionality is
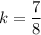 .
.