Question

What is the rule that defines the function represented by the table?

Answer 1

what is the rule that defines a function represented by the table. is it increasing or decreasing

Answer 2

The rule that defines the function represented by the table is:

• c.
  `f(x)=40((1)/(4))^(x)`

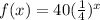
Explanation:

To identify the rule that defines the function represented by the table, you must know that
`f(x) = y`, so, you can take formula by formula and replace in it the values given in the table, if the result is equal to
`y` replacing the values of
`x`, you're gonna know that formula is correct. Let's do that exercise with the formulas in order:

• a.
  `f(x)=(1)/(4)(40)^(x)`

Now, we're gonna replace the variable
`x` by the first value in the table: 0

• 
  `f(x)=(1)/(4)(40)^(0)`
• 
  `f(x)=(1)/(4)*1`
• 
  `f(x)=(1)/(4)`

How you can see in the table, exactly below the value 0 to the variable
`x` is the value to
`y` (40), how the answer with the A option doesn't result in 40, it doesn't the correct rule.

• b.
  `f(x)=(1)/(2)(40)^(x)`

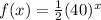
We replace with the value 0 again:

• 
  `f(x)=(1)/(2)(40)^(0)`
• 
  `f(x)=(1)/(2)*1`
• 
  `f(x)=(1)/(2)`

In this case, it neither gives us the value 40, for this reason, we pass to the next option:

• c.
  `f(x)=40((1)/(4))^(x)`

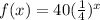
We replace with the value 0 one more time:

• 
  `f(x)=40((1)/(4))^(0)`
• 
  `f(x)=40*1`
• 
  `f(x)=40`

With this option, the result is equal to the first datum, but, to check this, we can replace the same formula with one or two values more:

• 
  `f(x)=40((1)/(4))^(1)`
• 
  `f(x)=40*((1)/(4))`
• 
  `f(x)=10`

• 
  `f(x)=40((1)/(4))^(2)`
• 
  `f(x)=40*((1)/(16))`
• 
  `f(x)=(5)/(2)`

How you can see, with the C option, once you replace the value of
`x`, the result is exactly the value for
`y`, for this reason, the C option is the correct answer.