Question

Make sure to abide by the difference quotient part of the question

Answer 1

We have to find the tangent line to y = x² - 3 at x = a.

The slope of the tangent line will be equal to the first derivative at that point.

We start by calculating the first derivative using the definition of the derivative:

`\begin{gathered} y^(\prime)=\lim_(h\to0)(f(x+h)-f(x))/(h) \\ y^(\prime)=\lim_(h\to0)((x+h)^2-3-x^2+3)/(h) \\ y^(\prime)=\lim_(h\to0)(x^2+2xh-h^2-x^2-3+3)/(h) \\ y^(\prime)=\lim_(h\to0)(2xh-h^2)/(h) \\ y^(\prime)=\lim_(h\to0)2x-h \\ y^(\prime)=2x \end{gathered}`

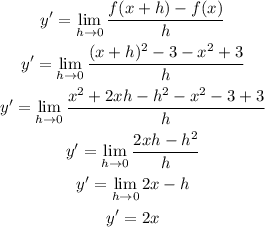
As we have to calculate the tangent line at x = 2 and a = 2, we can replace x with 2 to find the slope of the tangent line:

`m=y^(\prime)(2)=2(2)=4`

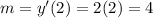
We now need a point of the line to find its complete equation.

As the line is tangent to (a, f(a)) we can calculate the value of f(a) = f(2) as:

`f(2)=(2)^2-3=4-3=1`

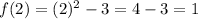
Then, with a slope m = 4 and tangent to point (2, 1) we can write the equation of the line as:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-1=4(x-2) \\ y=4x-8+1 \\ y=4x-7 \end{gathered}`

We can check this with a graph as:

Answer:

The tangent line is y = 4x - 7