Question

The table shows the height of a plant as it grows. Which equation in point ­slope form gives the plant’s height at any time

Time (months) Plant Height (cm)
2 16
4 32
6 48
8 64

A. y – 16 = 8(x – 2)
B. y – 16 = 8x – 2
C. y + 16 = 8(x + 2)
D.The relationship is nonlinear.

Answer 1

Option A is correct.

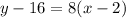`y-16=8(x-2)` is the equation represent the point slope form gives the plant's height at any time.

Explanation:

Point slope intercept form: For any two points
`(x_1, y_1)` and
`(x_2, y_2)` then,

the general form

`y-y_1=m(x-x_1)` for linear equations; where m is the slope given by:

`m =(y_2-y_1)/(x_2-x_1)`

Consider any two points from the table;

let A= (2 , 16) and B =(4, 32)

First calculate the slope of the line AB:

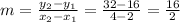`m =(y_2-y_1)/(x_2-x_1)=(32-16)/(4-2)=(16)/(2)` = 8

Therefore, slope of the line m = 8

Then,

the equation of line is:

`y-y_1=m(x-x_1)`

Substitute the value of m=8 and (2, 16) above we get;

`y-16=8(x-2)`

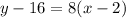
Therefore, the equation in point slope form which gives the plant's height at any time is;
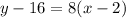`y-16=8(x-2)` , where x is the time(months) and y is the plant height (cm)