Question

I need help with my homework PLEASE CHECK WORK WHEN DONE NUMBER 4

Answer 1

From the question, we have that:

1. A large company claims that the average age of their employees is 32 years. In this case, we have the mean of the population, μ = 32 years.

2. The standard deviation for the population is 4 years, that is, σ = 4 years.

3. We have the average age of employees in the sales department is 27 years, that is, x(bar) = 27 years.

4. We know that the given data is approximately normal.

From this, we can standardize the age of the employees of the company by finding the z-score as follows:

`\begin{gathered} z=\frac{\bar{x}-\mu}{\sigma} \\ \text{ Therefore, we have:} \\ \\ z=(27-32)/(4)=-(5)/(4)=-1.25 \\ \\ z=-1.25 \\ \end{gathered}`

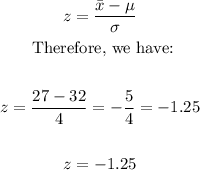
As we can see, we have a z-score of z = -1.25. This value is below the mean of the population. We can use this standard value to find the cumulative probability for it using the cumulative standard normal distribution.

We need to find the corresponding cumulative probability for z = -1.25, and we have, from the table:

Therefore, we have that the area under the normal curve below the standardized employee age is:

`P(z<-1.25)=0.10565`

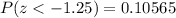
And we can represent this, graphically, as follows:

Using a graphing calculator, we have that the area under the normal curve below the standardized employee age is 0.105649773667.

Therefore, in summary, we can say that the area under the normal curve below the standardized employee age is, approximately, 0.1056 (option B).