Question

Explain with definition and example of Cross Product of Vectors.

Answer 1

Given:

Cross product of vectors.

Required:

To define and explain the cross product of vectors.

Step-by-step explanation:

Cross product is the binary operation on two vectors in three dimensional space. It again results in a vector which is perpendicular to both the vectors. Cross product of two vectors is calculated by right hand rule.

Right hand rule is nothing but the resultant of any two vectors is perpendicular to the other two vectors. Using cross product, we can also find the magnitude of the resulting vector.

Let

Vector A and Vector B is denoted by

`\vec{A}*\vec{B}`

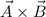
and its resultant vector is perpendicular to the vectors A and B.

Cross Product Formula :

`\vec{A}*\vec{B}=ab\sin\hat{\theta n}`

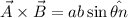
where n is the unit vector.

Example:

Let

`\begin{gathered} \vec{a}=2i+k \\ \vec{b}=i+j+k \end{gathered}`

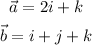
So,

`\vec{a}*\vec{b}=\begin{bmatrix}{i} & {j} & {k} \\ {2} & {0} & {1} \\ {1} & {1} & {1}\end{bmatrix}`
`\begin{gathered} =i(-1)-j(2-1)+k(2-0) \\ =-i-j+2k \end{gathered}`

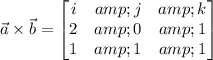
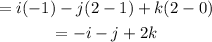
Final Answer:

Cross product is the binary operation on two vectors in three dimensional space.