Answer:
The prices of the two stocks will be the same in 1.56 hours.
Explanation:
The price of Stock A at 9 A.M. was $12.95 Since then, the price has been increasing at the rate of $0.12 each hour.
This means that after x hours, the value of Stock A is:

After noon:
Noon is 3 hours after 9 AM, so
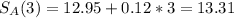
So in x hours after noon, the value is given by:
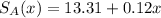
At noon the price of Stock B was $13.70. It begins to decrease at the rate of $0.13 each hour.
This means that after x hours, the value of Stock B is:
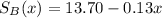
In how many hours will the prices of the two stocks be the same?
This is x for which:
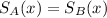
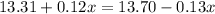
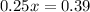
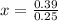
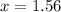
The prices of the two stocks will be the same in 1.56 hours.