Question

Given right triangle GYK, what is the value of tan(G)?

1/2
square root 3 / 2
2 square root 3 / 3
square root 3

Answer 1

(D)

Explanation:

It is given that GYK is a right angled triangle, which is right angled at K and the measure of the angle G is 60° and the measure of the angle Y is 30°.

Now, from the ΔGYK, using the trigonometry, we have

`tanG=(sinG)/(cosG)`

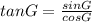
Now,the value of
`sinG` is :

`sinG=sin(60^(\circ))`

=
`(√(3))/(2)`

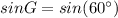
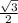
And, the value of
`cosG` is:

`cosG=cos(60^(\circ))`

=
`(1)/(2)`

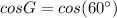
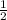
Now, the value of
`tanG` is:

`tanG=(sinG)/(cosG)`

`tan(60^(\circ))=(sin60^(\circ))/(cos60^(\circ))`

`tan60^(\circ)=((√(3))/(2))/((1)/(2))`

`tan60^(\circ)=√(3)`

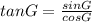
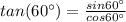
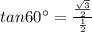
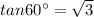
Thus, option D is correct.

Answer 2

we know that

`G=60\°`

The value of the tangent is equal to

`tan(G)=(sin(G))/(cos(G))`

remember that

`sin(60\°)=(√(3))/(2)`

`cos(60\°)=(1)/(2)`

substitute

`tan(60\°)=((√(3))/(2))/((1)/(2))`

`tan(60\°)=√(3)`

therefore

the answer is

square root 3