Question

the average number of phone inquiries per day at the poison control center is 4 find the probability it will receive 5 calls on a given day

Answer 1

Assuming a Poisson Distribution then probability it receives "k" calls is:

`P(x=k) = (\lambda^k e^(-\lambda))/(k!)`
where
`\lambda = 4, k =5`

Answer 2

Answer: The probability it will receive 5 calls on a given that is 0.15.

Explanation:

Since we have given that

The average number of phone inquires per day at the poison control centre = 4

So, λ = 4

Number of calls received on a given day = 5

so, k = 5

We will use "Poisson Distribution" to find the probability that it will receive 5 calls on a given day.

So, it will be written as

`P(X=k)=(\lambda^k.e^(-\lambda))/(k!)\\\\P(X=5)=(4^5* e^(-4))/(5!)\\\\P(X=5)=0.15`

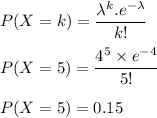
Hence, the probability it will receive 5 calls on a given that is 0.15.