Question

3. Given the recursive equation for each arithmetic sequence, write the explicit equation.

f(n)=f(n-1)-2; f(1)=8
f(n)=5+f(n-1);f(1)=0

Answer 1

Given:

The recursive formulae are:

(a)
`f(n)=f(n-1)-2; f(1)=8`

(b)
`f(n)=5+f(n-1); f(1)=0`

To find:

The explicit equation.

Solution:

A recursive formula of an arithmetic sequence is

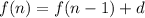`f(n)=f(n-1)+d` and f(1) is the first term.

Where, d is the common difference.

The explicit formula is

`f(n)=a+(n-1)d`

where, a is first term and d is common difference.

(a)

We have,

`f(n)=f(n-1)-2; f(1)=8`

Here, first term is 8 and common difference is -2. So, the explicit formula is

`f(n)=8+(n-1)(-2)`

`f(n)=8-2n+2`

`f(n)=10-2n`

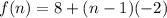
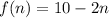
Therefore, the explicit formula is
`f(n)=10-2n`.

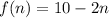(b)

We have,

`f(n)=5+f(n-1); f(1)=0`

Here, first term is 0 and common difference is 5. So, the explicit formula is

`f(n)=0+(n-1)(5)`

`f(n)=5n-5`

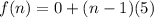
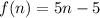
Therefore, the explicit formula is
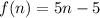`f(n)=5n-5`.