Answer: The work done for the given process is -778 kJ
Step-by-step explanation:
To calculate the amount of work done for an isothermal process is given by the equation:

W = amount of work done = ?
P = pressure of the container =
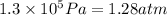 (Conversion factor:
(Conversion factor:
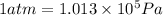 )
)
 = initial volume =
= initial volume =
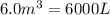 (Conversion factor:
(Conversion factor:
 )
)
 = final volume =
= final volume =
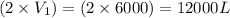
Putting values in above equation, we get:

To convert this into joules, we use the conversion factor:
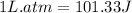
1 kJ = 1000 J
So,
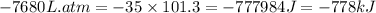
The negative sign indicates the system is doing work.
Hence, the work done for the given process is -778 kJ