Question

Use the table below to find each probability. The table gives information about students at one school.

Answer 1

Conditional Probabilities

The table gives us information about the favorite leisure activities of students at a school

We are required to find the probability of some events, given the occurrence of another event.

a) P(Sports | Female). It's the probability that a student likes sport if it's a female.

There are 334 female students, from which 39 like sports, thus:

`P(S|F)=(39)/(334)=11.68\text{ \%}`

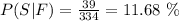
b) P(Female | Sports). It's the probability that a student is known to like sports and it's also a female.

There are 106 students that like sports, from which 39 are female, thus:

`P(F|S)=(39)/(106)=36.79\text{ \%}`

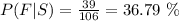
c) P(Reading | Male). It's the probability that a male student likes reading.

There are 366 male students from which 76 like reading, thus:

`P(R|M)=(76)/(366)=20.77\text{ \%}`

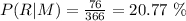
d) P(Male | Reading). It's the probability that a student is known to like reading and it's also a male. There are 161 students who like reading out of which 76 are male, thus:also a male. d)

`P(M|R)=(76)/(161)=47.20\text{ \%}`

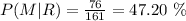
e) P(Hiking | Male). There are 366 male students out of which 58 like hiking, thus:H

`P(H|M)=(58)/(366)=15.85\text{ \%}`

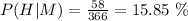
f) P(Hiking | Female). There are 334 female students out of which 48 like hiking, thus:

`P(H|F)=(48)/(334)=14.37\text{ \%}`

g) P(Male | Shopping). There are 139 students who like shopping and from them, 68 are male, thus:39 students who like shopping and fr

`P(M|S)=(68)/(139)=48.92\text{ \%}`

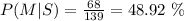
h) P(Shopping | Female). There are 334 female students from which 71 like shopping, thus:

`P(S|F)=(71)/(334)=21.26\text{ \%}`

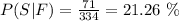
I) P(Phoning | Male). There are 366 male students from which 54 like phoning, thus:

`P(P|M)=(54)/(366)=14.75\text{ \%}`

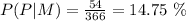
ich 39 are female, thus:

S