Question

Patients wait 126 days on average for a heart transplant with a standard deviation of 24 days. Whatproportion waits fewer than 90 days? (enter theanswer as a percent rounded to the nearesthundredth as needed)

Answer 1

6.68%

Explanation:

• Average Wait Period = 126 days

,

• Standard Deviation = 24 days

,

• X=90 days

First, we find the z-score using the z-score formula:

`\begin{gathered} z=(X-\mu)/(\sigma) \\ z=(90-126)/(24)=-(36)/(24)=-1.5 \end{gathered}`

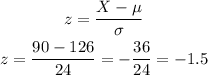
Next, we find the proportion that waits fewer than 90 days, i.e. P(z<-1.5).

From the z-score table:

`\begin{gathered} P(z<-1.5)=0.066807 \\ =6.68\% \end{gathered}`

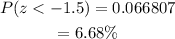
The proportion that waits fewer than 90 days is 6.68%.