Question

Can somebody help me with number 7

Answer 1

`x = 16.5`

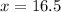
Explanation:

There is no number 7. The only complete question here is number 12 and the solution is as follows:

The attached figure is a right-angled triangle and the given parameters are:

`\theta = 70^(\circ)`

`Opposite = x`

`Adjacent = 6`

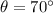
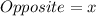
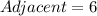
Required

Find x

The relationship between the given parameters is:

`tan(\theta) = (Opposite)/(Adjacent)`

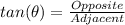
This gives:

`tan(70^(\circ)) = (x)/(6)`

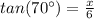
Multiply both sides by 6

`6 * tan(70^(\circ)) = (x)/(6)*6`

`6 * tan(70^(\circ)) = x`

`x = 6 * tan(70^(\circ))`

`tan(70^(\circ)) = 2.7474`

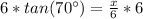
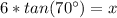
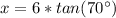
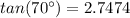
So, we have:

`x = 6 * 2.7474`

`x = 16.4844`

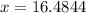
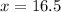`x = 16.5` -- approximated